PTC ist die Abkürzung für Positive
Temperature Coefficient,
was soviel bedeutet wie Halbleiterwiderstand mit einem positiven Temperaturverhalten.
Der PTC wird auch Kaltleiter genannt, da er bei niedrigen Temperaturen einen
elektrischen Strom besser leitet, als bei hohen Temperaturen. Die Grundkennlinie
eines PTC lässt sich umfänglich nicht deterministisch beschreiben.
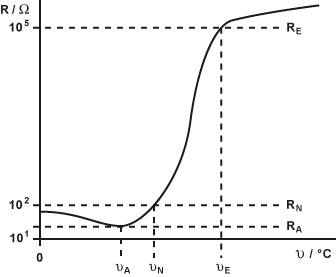
In diesem Diagramm sind drei Teilbereiche erkennbar.
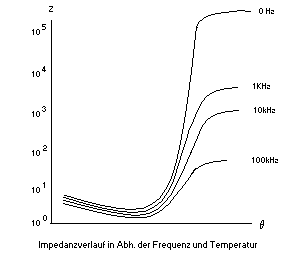
Weiterhin gilt üblicherweise: RN = 2 x RA und im Bereich zwischen RN und RE kann der Widerstand mittels RNE = R0eb(T-T0) beschrieben werden. (b ist die Materialkonstante und R0 ist der Nennwiderstand bei Nenntemperatur T0). Die gezeigte Kurve gilt jedoch nur für sehr niedrige Messspannungen - üblicherweise UPTC <= 1.5V. Dies hat den Hintergrund, dass bei höheren Spannungen eine Eigenerwärmung des PTC (PPTC=U2/R) erfolgt und dies Einfluss auf den Kurvenverlauf hat. Der PTC ist aufgrund seiner internen Struktur auch frequenzabhängig. Ab einer beaufschlagten Frequenz oberhalb von 1MHz hat der PTC eine Impedanz nahe 0. PTC sollten daher nur bei niedrigen Frequenzen eingesetzt werden. Die nachfolgende Grafik veranschaulicht das Frequenzverhalten eines PTC.

- fallender Widerstand bis zum Punkt θA
- steil ansteigender Widerstand ab θN bis zum Punkt θE
- abknickender, flach ansteigender Widerstand ab dem Punkt θE
Weiterhin gilt üblicherweise: RN = 2 x RA und im Bereich zwischen RN und RE kann der Widerstand mittels RNE = R0eb(T-T0) beschrieben werden. (b ist die Materialkonstante und R0 ist der Nennwiderstand bei Nenntemperatur T0). Die gezeigte Kurve gilt jedoch nur für sehr niedrige Messspannungen - üblicherweise UPTC <= 1.5V. Dies hat den Hintergrund, dass bei höheren Spannungen eine Eigenerwärmung des PTC (PPTC=U2/R) erfolgt und dies Einfluss auf den Kurvenverlauf hat. Der PTC ist aufgrund seiner internen Struktur auch frequenzabhängig. Ab einer beaufschlagten Frequenz oberhalb von 1MHz hat der PTC eine Impedanz nahe 0. PTC sollten daher nur bei niedrigen Frequenzen eingesetzt werden. Die nachfolgende Grafik veranschaulicht das Frequenzverhalten eines PTC.

Einsatz als Schutzelement in Schaltungen:
Der PTC wird sehr häufig als Schutzelement eingesetzt. Wie bereits erwähnt
kommt es beim PTC und höheren Spannungen zur Eigenerwärmung. Dies wiederum
bedingt eine Änderung des Widerstandes. Die nachfolgende Grafik verdeutlicht
das Verhalten des PTC in einer Strom-Spannungs-Kennlinie.
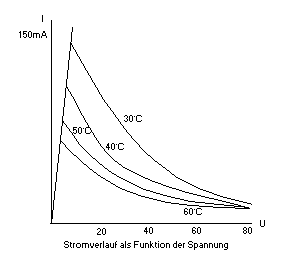
Im unteren Spannungsverlauf verhält sich der PTC recht linear - also fast
wie ein ohmscher Widerstand. Bei höheren Spannungen kommt es aufgrund der
Eigenerwärmung zum starken, nichtlinearen Anstieg des Widerstandes, was sich
in der Grafik als Strombegrenzung bemerkbar macht. Diese Strombegrenzung ist weiterhin
noch von der Umgebungstemperatur abhängig, die zusätzlich zur Eigenerwärmung
wirkt. Die Angaben in der Grafik gelten für keine bis geringe Konvektion.
Das Einsatzgebiet des PTC kann sich über

- Motorenschutz
- Strombegrenzung / rückstellende Sicherung
- bedingte Temperaturregelung
- Verzögerungsschaltelement
Kennlinienlinearisierung:
Mittels Kennlinienlinearisierung kann der PTC auch für Temperaturmessungen
in einem bestimmten Messbereich eingesetzt werden. Die Auswertung kann dann
über einen Mikrocontroller mit A/D Wandler ohne Umrechnung mittels Tabelle
erfolgen. Das nachfolgende Bild zeigt die Grundschaltung für die
Linearisierung:
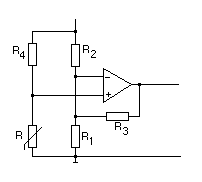
Nun werden die Widerstandswerte berechnet. Dazu muß vorher definiert werden,
in welchem Temperaturbereich die Linearisierung erfolgen soll. Hierzu werden
einfach 3 Temperaturen bestimmt und die dazugehörigen Widerstandswerte laut
PTC-Kennlinie ermittelt. Die niedrigste Temperatur im Messbereich wird
θU genannt, die oberste Temperatur im Messbereich wird
θO genannt und die exakt in der Mitte liegende Temperatur
wird dann θM genannt. Über die Kennlinie werden dann die
passenden Widerstandswerte RU, RO und RM
ermittelt. Daraus ergibt sich der Linearisierungswiderstand R4 nach
folgender Formel:
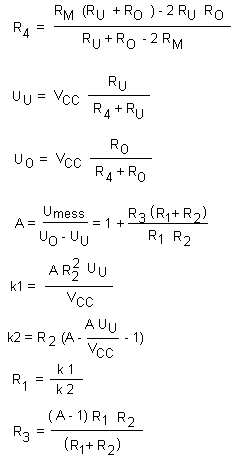
Weiterhin wird vorgegeben, dass der Widerstand R2 identisch mit dem
Linearisierungswiderstand R4 ist. Nun wird noch die Verstärkung
der Beschaltung berechnet. Dazu muss jedoch der Spannungsbereich Umess
am Ausgang des Operationsverstärkers definiert werden. Dieser liegt
notwendigerweise in einem Bereich, den der A/D Wandler noch messen kann.
Weiterhin sollte der Bereich so groß gewählt werden, dass eine entsprechende
Auflösung erreicht wird. Nachdem R4 nun bekannt ist, kann damit
die untere und obere resultierende Spannung UU und UO
am PTC berechnet werden. Danach wird der Verstärkungsfaktor A laut Formel
berechnet. Schließlich können die restlichen Widerstände R1 und
R3 berechnet werden. Damit sind alle Bauteilwerte für die Schaltung
bekannt.

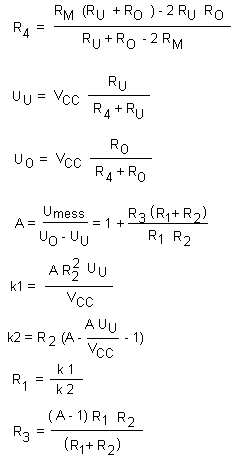
Beispielapplikation:
Das Ing.-Büro Kirchen hat einen kundenspezifischen und busfähigen
8 Kanal Temperaturwächter
für die Überwachung von Motortemperaturen auf PTC Basis entwickelt.
Informieren Sie sich auch einmal auf der Produktseite Automatisierung nach weiteren Kundenentwicklungen.
Informieren Sie sich auch einmal auf der Produktseite Automatisierung nach weiteren Kundenentwicklungen.
Dann nehmen Sie gleich Kontakt mit uns auf oder informieren Sie sich über unser Entwicklungsangebot